最近几周,我见了多家客户,涉及到航空、仓储、制造多个行业,在与他们交流生产交期预测、安全库存设置,以及价格预估的过程中,我猛然想到了一个诠释“分析即聚合”以及“高级分析”的绝佳视角,得以把业务的需求与技术的实现方式深度结合起来。
这将是《业务分析通识》极其具有启发性的内容,本文将结合《数据可视化分析(第2版)》的内容先做诠释。
一、理解分析的本质:抽象与聚合
在之前的多篇文章中,我用多个视角诠释了分析的本质过程。在这里不再赘述类似内容。读者可以先观看如下的两篇文章:
概括而言,
- 数据查询和数据分析的关键差异在于:分析是对业务及数据的高度抽象过程
- 最重要的数据抽象方式是聚合函数及其计算,因此说“聚合是分析的本质”,分析即聚合
- 整个计算的体系,可以围绕聚合展开:行级别与聚合,聚合前筛选与聚合后筛选,聚合前预先聚合与聚合后二次聚合等
本文聚焦业务中的指标分类,不同抽象程度的指标借助于不同形式的聚合函数完成。
二、从问题分类,到指标的分类体系
在问题的基本结构中,问题答案是关键,对应技术上的聚合计算,另外的两个构成部分都围绕问题答案而有价值——问题详细级别是答案的分组依据,分析范围则决定答案的样本范围。

在业务分析中,哪些管理中普遍使用的聚合计算常常被称之为“指标”并约定俗称,成为公司管理者探究业务变化、跟踪业务决策的重要抓手。这些指标无一例外的使用了聚合计算,我们可以根据聚合计算的复杂性,把它们划分为如下的几个类型:
- 一类指标:以直接聚合及其四则运算为实现方式,比如销售额总和、平均销售数量
- 二类指标:基于直接聚合的二次计算,比如合计销售均价、利润率等,一些常见的计算会进一步固化为函数,比如标准差
- 三类指标:指标计算中包含不同的范围,比如YTD金额、去年同期金额,以及建立在此基础上的二次计算,比如年度同比、月度环比、客户迁徙M0-M1%、合计百分比等
- 四类指标:包含排序、累计等行间计算的指标,比如TOP10产品占比、物料集中度(单一客户占比超过50%的物料数量,在所有物料中的占比)。
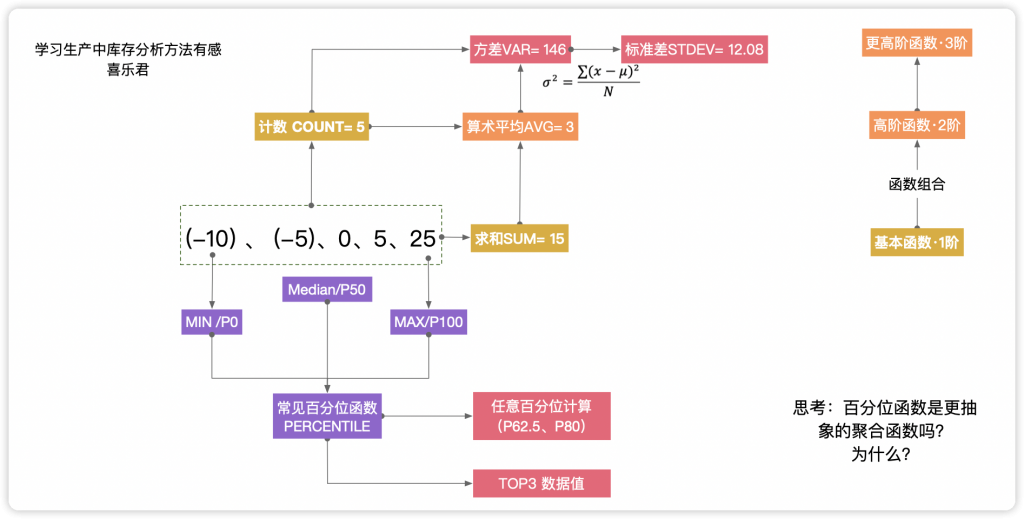
三、理解聚合的实现形式:聚合函数
甚至可以按照计算的复杂性,把聚合函数分为不同的阶段:
- 1阶函数:sum和count,代表总体规模
- 2阶函数:avg平均值,代表抽象特征,是sum和count的组合形式
- 3阶段函数:var方差,代表更抽象特征,描述波动情况,是数据值及avg和count的组合形式
- 4阶段函数:max、min、percentile等百分位函数,在聚合过程中包含了相互之间的比较,性能上运算更慢,用个体描述总体特征。 为了方便理解,可以把MAX等包含排序过程的函数,理解为self-join的自连接过程。这将有助于理解。
下文摘自《数据可视化分析(第二版):分析原理与Tableau、SQL实践》第八章
8.5 分析函数:从明细到问题的“直接聚合”
行级别计算是为问题分析而做的准备。分析必然包含聚合,“聚合就是从数据表的行级别到问题级别的由多变少的过程”,为了和后续的表计算等间接聚合相区别,这里介绍的聚合称之为“直接聚合”。
常见的直接聚合函数包括总和SUM、平均值AVG、最大值MAX、最小值MIN、重复计数COUNT、不重复计数COUNTD(COUNT DISTINCT)、中位数MEDIAN等。大数据分析中,还有衡量离散程度的方差、体现个体位置的百分位等函数,这里分类介绍。
8.5.1 描述规模:总和、计数、平均值
最常见的分析需求是衡量数据值有多少(规模),代表函数是求和SUM、计数COUNT,分别对应数据表中数字、字符串数据类型的字段列。其中,计数又可以分为重复计数(COUNT)、不重复计数(COUNT DISTINCT)两类。举例:
- 数字型字段求和聚合:销售额总和-SUM([销售额]) 、 利润总和-SUM([利润])
- 字符串字段计数(重复计数):客流量-COUNT([客户ID])
- 字符串字段计数(不重复计数):客户数-COUNTD([会员ID])、订单数COUNTD([订单ID])
数字默认聚合,默认聚合方式是SUM求和,在问题中,默认聚合方式常被忽略,影响了初学者理解“聚合是分析的本质”,比如“各类别的销售额(总和)”。本书中,笔者尽可能补全聚合方式。
很多字段的求和没有分析意义,比如年龄、发货间隔等,这种属性称之为“不可加性”(non-additive),此时平均值AVG聚合通常就是首选的聚合方式,用以代表年龄、发货周期的总体特征。
在Tableau中,数字型字段的默认聚合都是求和SUM,分析师可以更改字段的默认聚合方式,或者在视图中临时调整。如图8-32左侧所示,在字段【发货间隔】上右键,在弹出的下拉菜单中,选择“默认属性→聚合→平均值”,以后双击该字段,默认都是“平均值AVG”。也可以在视图中,临时调整字段聚合方式,如图8-32右侧所示,点击聚合的字段右键,在弹出的下拉菜单中,从“度量”列表中切换聚合方式即可。
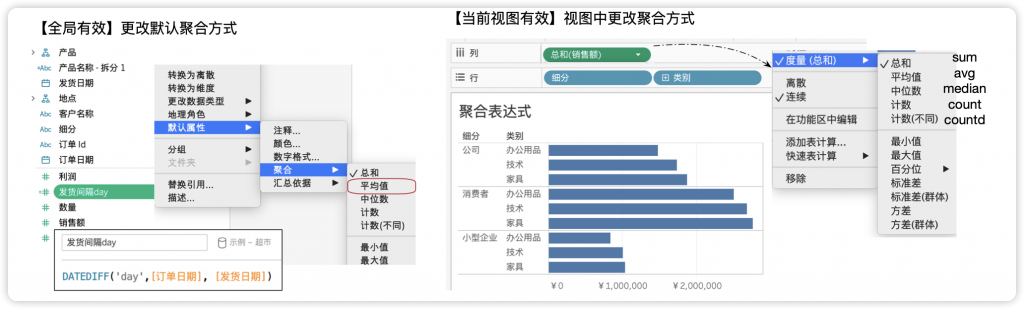
图8-32 为字段设置默认聚合方式,或者在视图中更改
正如8.1小节所述,不同的工具聚合语法略有不同,但聚合过程都一致。图8-33中展示了Excel、SQL和Python使用SUM函数求和的语法。
Tableau和SQL相比,差异较大的是不重复计数。SQL不重复计数是COUNT(DISTINCT [字段]),对应Tableau的COUNTD函数。
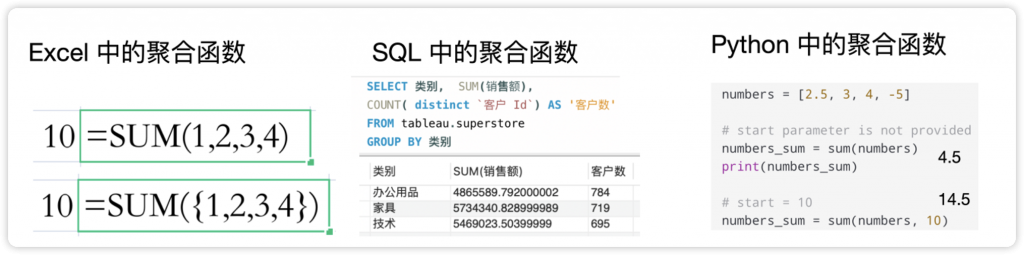
图8-33 不同工具中的聚合语法(注意明细行的多值相加和跨行相加的区别)
在业务分析中,衡量业绩绝对规模是基本的出发点。SUM、AVG、COUNT、COUNTD函数是构建“绝对规模”指标的聚合方式。商业仪表板内容的首要内容,基本都会被销售额总和、利润总和、平均交付周期、订单数等字段占据。
8.5.2 描述数据的波动程度:方差和标准差
总和、平均值、计数聚合常用于描述宏观特征,不考虑个体差异及其分布特征,因此容易受极大值、极小值等特殊值影响。在宏观指标之外,分析还要关注样本中个体的波动性(离散程度)及关键个体(如最大值、中位数、众数、最小值等)。描述波动程度的聚合方式是方差和标准差。
波动分析在质量分析领域应用广泛,质量控制图、西格玛分布图与此有关。
方差(variance)用于衡量数据的离散程度。总体方差( )是总体数据中各样本数据和总体平均数( )之差的平方和的平均数,公式如下所示:
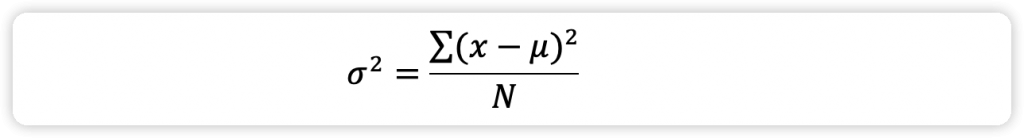
注: 为为总体方差,x为每个数据值,μ为总体均值,N为数据数量
方差相当于以总体的平均数( )为基准,计算每个数据的偏移。相同的多个数据,方差就是0;随着数据围绕基准波动,方差就会增大。为避免上下完全相反的波动相互抵消,比如{4,5,5,6},方差使用了2次方计算偏离。
举例:
- {5,5,5,5} =0/4=0 (无波动)
- {4,5,5,6} =2/4=0.5 (出现了波动)
- {3,4,6,7} =10/4=2.5 (波动进一步增大)
为了更形象地说明,这里用一组身高数据计算方差。如图8-34所示,4个人的身高数据为{190,170,165,160}(单位cm),平均数为170,方差为131.25。如果身高全部减少10厘米,平均数变化,但方差不变。
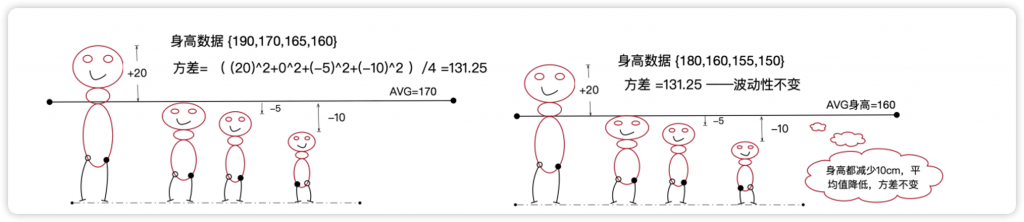
图8-34 4个人身高的离散程度——使用方差量化
可见,方差虽然建立在平均值基础上,但是又截然不同。方差越大,代表离散程度越高,但不代表总体的平均身高情况。
由于方差使用“差异”的平方来计算,难以将方差和数据值直接比较。为了保持与样本数据单位的一致性,就有了它的平方根形式——标准差(standard deviation)。在于数据值比较时,标准差比方差更直观、易于理解。
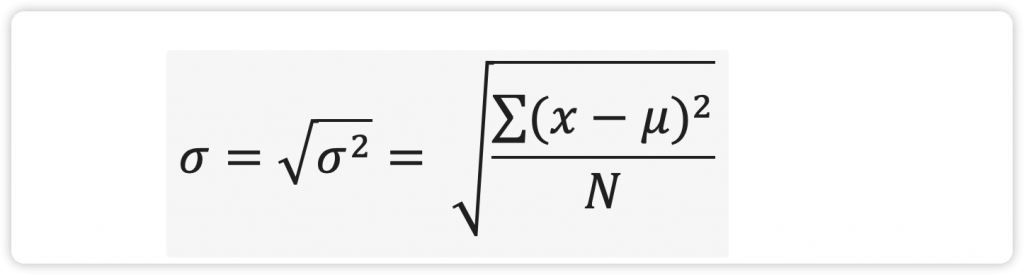
比如,4个人身高的方差是131.25,对应标准差是11.45,这是量化后的平均波动范围。如图8-35所示,有3个人的身高在平均值上下1个标准差范围之内(即170 11.45),即“1个标准差”范围( 1σ西格玛)。
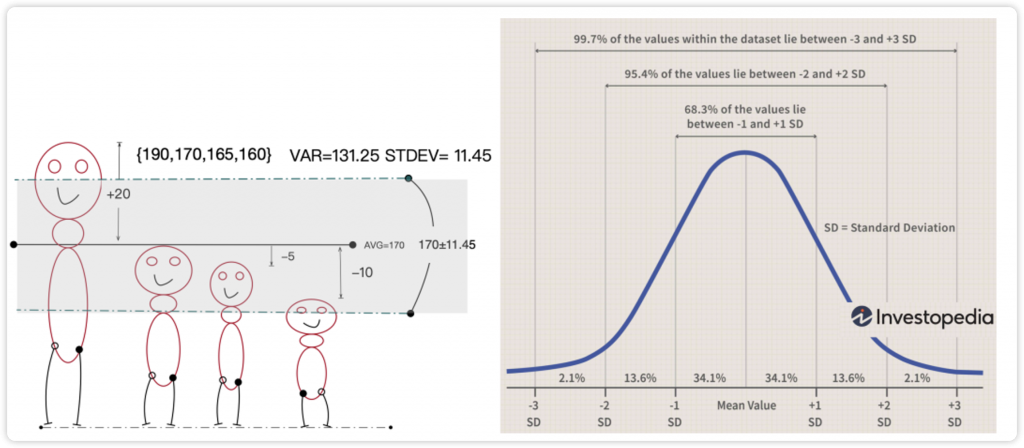
图8-35 使用标准差有助于更好地衡量分布
如图8-35右侧所示,在标准的正态分布中,1西格玛的概率是68.3%,3西格玛是99.7%。精益质量管理中常用的“六西格玛”方法,就是将质量缺陷控制在3.4ppm(百万分之3.4)之内。
这里以超市数据为例。图8-36展示了“2020年12月各地区交易的利润分析指标”。其中西南和华东区域交易的利润波动最大,借助它们的利润最小值和最大值也能部分佐证。
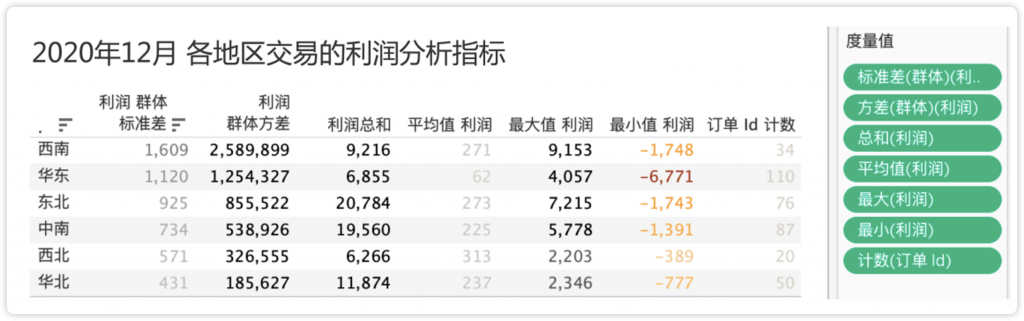
图8-36 2020年12月各地区交易的利润分析指标[1]
相比求和、平均值,方差的应用较少,集中在质量分析、采购价格波动分析等少数场景。简单的分析可以直接使用方差计算,复杂的应用都是基于聚合值的二次分析,常见的二次聚合则被简化到“分析”窗格中。在本书第5章5.4.3小节(参考区间、盒须图、标准差分布),质量控制图(一个标准差区间)就是基于标准差计算而生成的可视化。
8.5.3 关注个体、走向分布:百分位函数及最大值、最小值、中位数
分析通常是“分析宏观特征、不关注个体差异”,因此总和、平均值、计数是使用最频繁的聚合方式。业务探索分析的趋势是把宏观分析和微观分析紧密结合在一起,因此需要“关注个体”的分析指标,其中的典型代表是百分位数(percentile,符号为P),而百分位数的代表就是最小值、中位数和最大值,分别可以用P0、P50和P100代表。
关于“百分位数”的理解和计算,虽然没有统一,但不影响大家使用。Excel和Tableau都可以使用PERCENTILE()函数计算一组数据的百分位数,如图8-37所示。
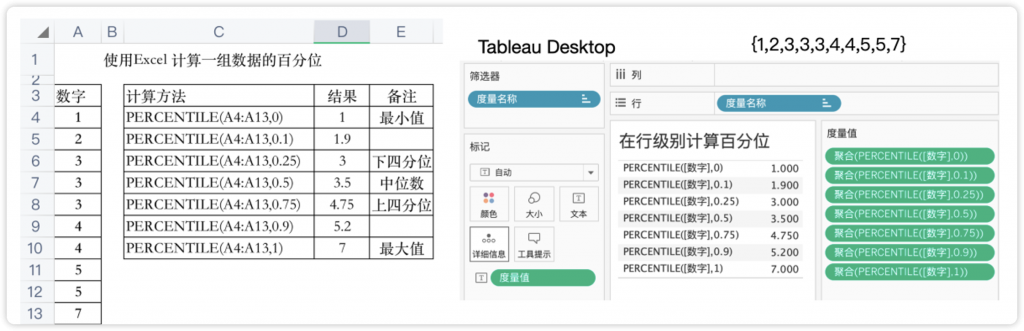
图8-37 使用Excel和Tableau计算一组数据的百分位
相对于此前的求和、求平均值,标准差和百分位数目前在业务分析中尚未普及,它们是分布分析的基础。有以下几个地方需要强调。
1.百分位数与常见聚合的关系
最大值MAX、最小值MIN、中位数MEDIAN是特殊的百分位数聚合,对应如下。
- 最大值MAX = 百分位数P100对应的数据 = PERCENTILE([销售额],1)
- 中位数MEDIAN = 百分位数P50对应的数据 = PERCENTILE([销售额],0.5)
(奇数序列即中间值,偶数序列则为中间两个数的平均值) - 最小值MIN =百分位数P0对应的数据 = PERCENTILE([销售额],0)
另外两个使用最广泛的是P25百分位和P75百分位,它们是“箱线图”分布的基础。图8-38展示了“2021年12月,各地区的(所有交易)利润分布”,使用百分位数展示了多个指标的计算。
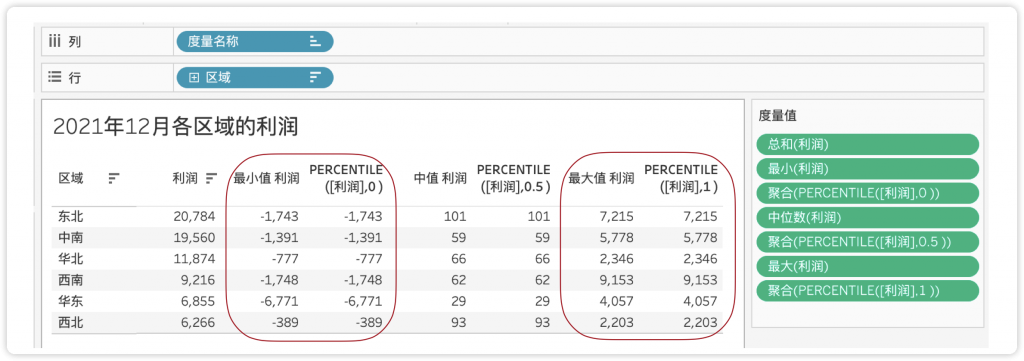
图8-38 2020年12月各地区所有交易明细的利润分布
上述文本表聚合难以对比,可视化的魅力在于借助位置、大小、形状等方式直观展现,图8-39展示了不同区域的利润箱线图分布(延伸到最大最小值)。可见华东地区的最小值P0最低(-6771),西南地区的最大值P100最高(9153);按照最大值和最小值的范围估计,华北地区的离散程度明显低于其他各地区。
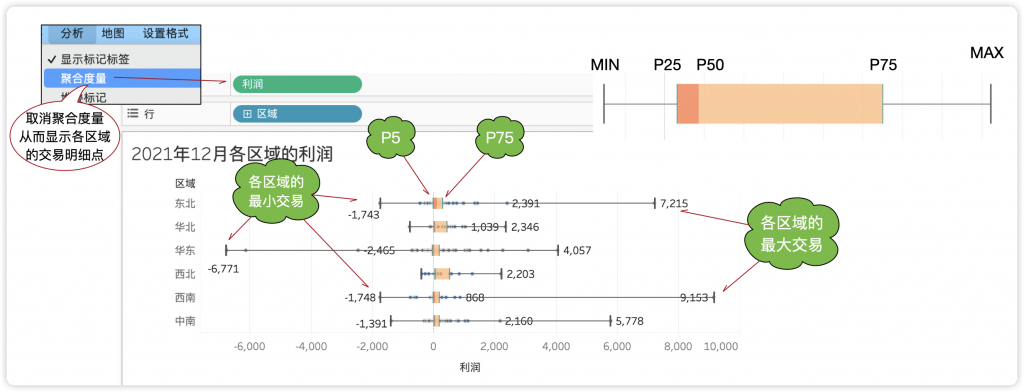
图8-39 2020年12月各地区的利润交易明细箱线图
取消默认的“聚合度量”,相当于从交易明细中构建了箱线图分布。业务中常见的箱线图分布是已有聚合值的二次抽象聚合,因此需要使用表计算完成,本书将在第9章9.7.4小节介绍。
2.百分位数、百分比与累计百分比的差异
百分比(percent,符号%)是相对于单一静态数值的算术计算,而百分位数(percentile,符号P)则是相对于多个数据点的聚合分布,如图8-40所示。
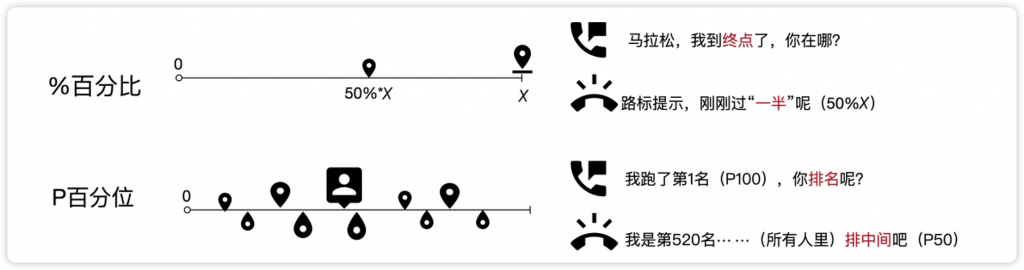
图8-40 百分比与百分位数
除了百分比、百分位,高级分析时常还会用到“累计百分比”,最典型的是帕累托分析中的“前20%的客户累计贡献了前80%的销售额总和”场景,和这里“百分比”不同,它是聚合值的二次计算,是第9章表计算的典型场景,本书将在第9章9.9小节介绍。
8.5.4 ATTR属性——针对维度字段的聚合判断
在Tableau分中,还有一个特殊的聚合方式:属性ATTR()函数。专门用于在视图中对字符串做唯一性判断。做出聚合字段,它受视图详细级别影响。
在Tableau中,“属性”ATTRIBUTION被用来代表视图详细级别对应的唯一值,比如男/女、户籍地是员工ID的性别属性、出生地属性。如果一个人有多个手机号,手机号就不是一个人的属性,此时ATTR函数就会返回星号“*”,都在该值不唯一。
如图8-41所示,左侧“客户名称”构成了问题详细级别的一部分,而在右侧,“客户名称”从维度改为“属性”,此时每个订单ID成为了问题详细级别,对应唯一的行。如果一个订单ID对应多个客户(这通常是数据采集的问题),那么就会返回“*”星号。
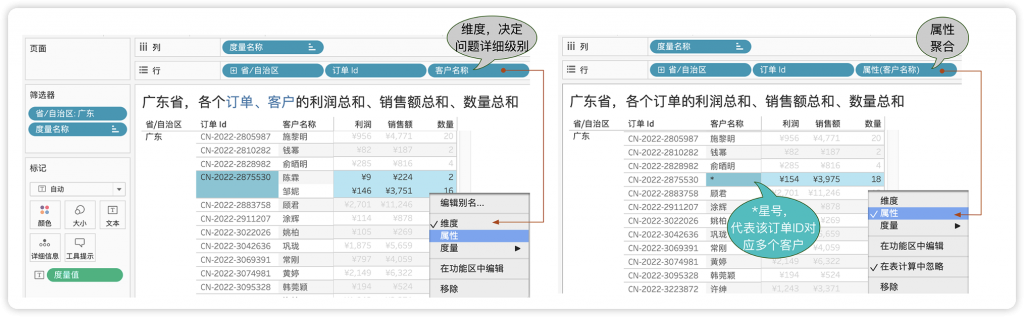
图8-41 ATTR函数返回离散维度的唯一值
初学者可以把ATTR([订单ID])理解为一个判断,这个判断有多种写法,旨在判断是否重复:
IF MAX([订单ID])=MIN([订单ID]) THEN MIN([订单ID]) ELSE '*' END在分析过程中,经常遇到“聚合和非聚合不能直接比较”的报错提醒,一个解决方案就是把明细判断改为聚合判断,或者聚合判断改为行级别,比如:
IF ATTR([子类别])= "桌子" THEN SUM([销售额])<1000 END
SUM(IF [子类别]= "桌子" THEN [销售额] END ) <1000使用ATTR聚合的前提是视图中有【子类别】字段,性能好但不易于控制;使用行级别判断把计算改到明细上完成,易于理解,但性能非常差。选择时要注意。
[1] 此处的“群体方差”就是“总体方差”,属于软件的翻译bug,已经申请修改,正在陆续调整。